LES NOMBRES RELATIFS

• Où trouve-t-on des nombres relatifs ?
• températures (-10°C à Reims en Hiver)
• soldes (-20% sur tel article)
• compte bancaire (compte débiteur de -50 €)
• bourse (1,5 % à la clôture)
• piles (pôle et pôle )
• Définition

L'ensemble des nombres positifs (4 ; 0 ; 57 ; 19,1...) et l'ensemble des nombres négatifs forment les nombres relatifs.

On peut placer des points sur une droite grâce à leurs abscisses. Une abscisse est un nombre relatif.

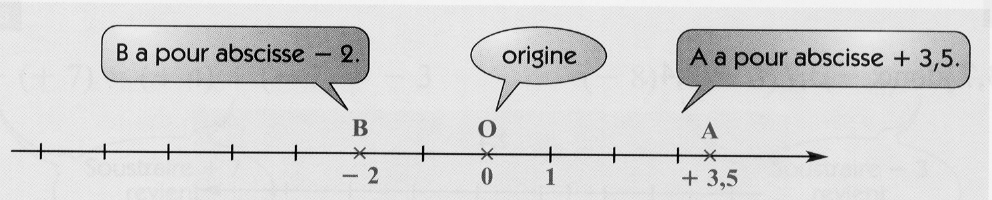
Remarquons, au passage, que placer des points sur une droite graduée permet de classer les abscisses de ces points. Ici,

La distance de à 0 est .

La distance de à 0 est

• Nombres opposés :

Deux nombres sont à la distance de zéro : les nombres et . Ce sont des nombres opposés.

Définition :

Deux nombres ayant la même partie numérique (ou distance à zéro) et des signes différents sont dits opposés.

Deux points ayant des abscisses opposées sont symétriques par rapport à l'origine :

• Comparaison de deux nombres relatifs :
• Nombres de signes différents :

La représentation des nombres relatifs sur une droite permet de visualiser l'ordre : le point est situé « à gauche » de donc .

Propriété :

Tout nombre négatif non nul est inférieur à zéro et tout nombre positif non nul est supérieur à zéro.

Tout nombre négatif non nul est inférieur à tout nombre positif.

• Nombres négatifs :

Propriété

De deux nombres négatifs, le plus grand est celui qui est le plus proche de zéro.

Ici, donc

• Addition de deux nombres relatifs :
• Nombres de même signe :

Propriété :

Pour additionner deux nombres relatifs de même signe :

• on garde le signe commun.
• on additionne les parties numériques.

Exemples :

• Nombres de signes différents :

Propriété :

Pour additionner deux nombres relatifs de signes différents :

• on repère celui qui a la plus grande partie numérique et on garde son signe.
• On soustrait la partie numérique de l'autre.

Exemples :

• Soustraction de deux nombres relatifs :

Propriété :

Pour soustraire un nombre relatif, on ajoute son nombre opposé.

• Simplification de notation :

Cas où le deuxième terme est positif

On rappelle que se note 3 et se note .

Cas où le deuxième terme est négatif

On transforme l'expression pour que le deuxième terme soit positif.

• Interprétation des notations simplifiées :

Pour calculer en notation simplifiée, on interprète l'expression à l'aide d'une addition :

• Distance de deux points sur une droite graduée :

L'abscisse d'un point sur une droite graduée est souvent notée .

Propriété :

La distance entre deux points et d'une droite graduée s'obtient par :

« plus grande abscisse » « plus petite abscisse ».

Exemple 1 : et

donc donc

Exemple 2 : et

donc donc

Remarque : dans tous les cas, la distance est positive.

• Repérage dans le plan :

A l'aide de deux axes gradués, chaque point du plan peut être repéré par deux nombres relatifs.

Dans le repère ci-dessous, les coordonnées de sont . On note : .

La première coordonnée de s'appelle l'abscisse de et elle est repérée sur l'axe horizontal appelé axe des abscisses. L'abscisse de est .

La deuxième coordonnée de s'appelle l'ordonnée de et elle est repérée sur l'axe vertical appelé axe des ordonnées. L'ordonnée de est .

Le couple (abscisse, ordonnée) s'appelle les coordonnées du point.

• calculer une somme algébrique :

Calculer

On repère les nombres négatifs et les nombres positifs en les regroupant, puis on ajoute les nombres positifs entre eux et les nombres négatifs entre eux :

• Calculer avec des parenthèses :

Calculer

On calcule à l'intérieur de chaque parenthèse en faisant attention aux signes :