
4ème chapitre 8:
PROBABILITES
I) VOCABULAIRE
1) Expérience aléatoire
Définition:
Une expérience est dite « aléatoire » si elle vérifie deux conditions :
- Elle conduit à des résultats possibles qu'on est parfaitement capable de nommer
- On ne sait pas lequel de ces résultats va se produire quand on réalise l'expérience.
Exemple :
On lance une pièce de monnaie et on regarde sur quelle face elle tombe. Cette expérience est aléatoire car :
- il y a deux résultats possibles : « PILE » « FACE »
- quand on lance une pièce on ne sait pas sur quelle face elle va tomber.
2) Evénement
Une possibilité de résultat est appelée issue.
Exemple :
On lance un dé à 6 faces et on observe la face obtenue. "obtenir 5" ou "obtenir 3" sont des issues. Il y a ici 6 issues possibles.
Un événement est composé de plusieurs issues.
« obtenir 2 » ou « obtenir 4 » ou « obtenir 6 »
Un événement élémentaire n'est composé que d'une seule issue.
Si toutes les issues ont la même chance de se réaliser, la situation est équiprobable.
le vocabulaire en vidéo
II) PROPRIETES
Propriété :
Si on répète une expérience aléatoire un très grand nombre de fois, la fréquence de n'importe quel événement de cette expérience finit par se stabiliser autour d'un nombre qui est la probabilité de cet événement.
Cette probabilité est la « chance » qu'un événement a de se produire.
Exemple( la théorie) :
« On dispose d'une urne qui
contient 2 boules jaunes et 3 boules rouges on tire une boule au hasard
et on s'intéresse à la couleur de la boule tirée. »
Si on renouvelle
un très grand nombre de fois cette expérience en remettant chaque fois
la boule tirée dans l'urne, la fréquence du résultat « la boule est
jaune » se stabilise autour de qui est la probabilité de l'événement
« Obtenir une boule jaune ».
Si on tire au hasard une boule
dans un sac contenant 8 boules dont 3 sont rouges et 5 sont vertes, la
probabilité de tirer une boule rouge est de 3/8
car on a 3 « chances » sur 8 de tirer une boule rouge.
Propriétés :
- La probabilité d'un événement est la somme des probabilités des événements élémentaires qui le composent.
- La probabilité d'un évènement est comprise entre 0 et 1.
- La somme des probabilités de chaque issue d'une expérience aléatoire est égale à 1.
Vocabulaire :
On dit qu'un événement est impossible lorsque cet événement est sûr de ne pas se produire. Sa probabilité est donc de 0.
- On dit qu'un événement est certain lorsque cet événement est sûr de se produire.
Sa probabilité est donc de 1.
Quand les résultats d'une expérience aléatoire ont tous la même
probabilité alors la probabilité d'un événement est égale au quotient :
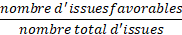
Si on tire au hasard une boule
dans un sac contenant 8 boules dont 3 sont rouges et 5 sont vertes, la
probabilité de tirer une boule rouge est de 3/8
car on a 3 « chances » sur 8 boules au total, de tirer une boule rouge.
Propriétés :
- La probabilité d'un événement est la somme des probabilités des événements élémentaires qui le composent.
- La probabilité d'un évènement est comprise entre 0 et 1.
- La somme des probabilités de chaque issue d'une expérience aléatoire est égale à 1.
Vocabulaire :
On dit qu'un événement est impossible lorsque cet événement est sûr de ne pas se produire. Sa probabilité est donc de 0.
- On dit qu'un événement est certain lorsque cet événement est sûr de se produire.
Sa probabilité est donc de 1.
Exemple : Un sac contient des boules blanches et noires et si la probabilité d'obtenir une boule noire est de 2/5 alors la probabilité d'obtenir une boule blanche est de 1-2/5=3/5.
III) Représentation d'expériences à plusieurs épreuves
On peut représenter une expérience aléatoire par un arbre des probabilités. Il servira à clarifier la situation et aura comme premier intérêt d'être très efficace.
1) Arbre de probabilité simple
Définition : Un arbre de probabilité est un arbre des issues qui est pondéré par des probabilités.
exemple 1:
On considère l'expérience aléatoire
suivante : on lance un dé cubique dont les faces
sont numérotées de 1 à 6. On suppose
que le dé n'est pas pipé, on est donc dans
une situation d'équiprobabilité.Les issues possibles sont : 1 ; 2 ; 3 ; 4 ; 5 ; 6.Les probabilités associées à chacune
de ces issues sont : 1/6
L'arbre des probabilités est donc :
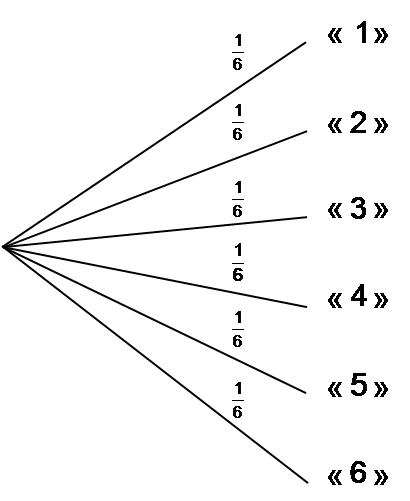
On considère une urne contenant 8 boules indiscernables au toucher.
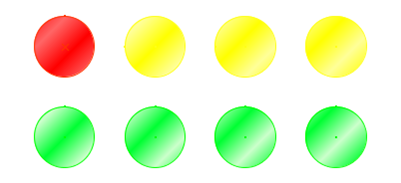
On tire une boule au hasard.
- Quel est le nombre d'issues possibles ? il y a 8 issues possibles.
- Une boule est rouge, trois sont jaunes et quatre sont vertes. On tire une boule et on s'intéresse à la couleur.
Il y a 3 événements possibles :
R : « obtenir une boule rouge ».
J : « obtenir une boule jaune ».
V : « obtenir une boule verte ».
Pour l'événement R, il y a 1 tirage favorable.
Pour l'événement J, il y a 3 tirages favorables.
Pour l'événement V, il y a 4 tirages favorables.
En inscrivant les probabilités associées sur chaque branche de l'arbre des possibles, on obtient : un arbre pondéré
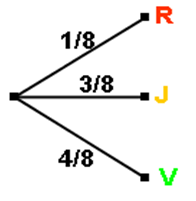
2) Arbre de probabilité
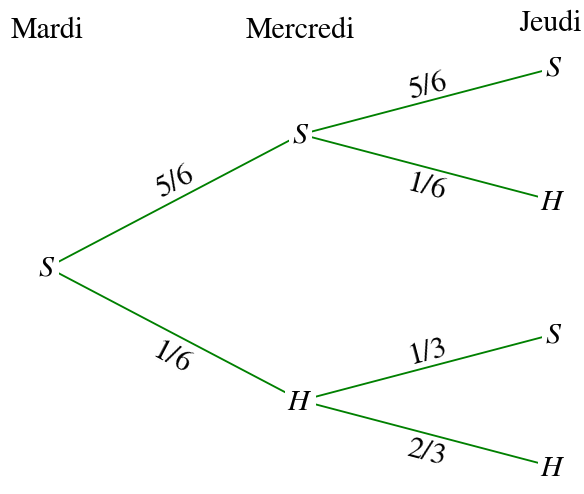
Exemple :Nous sommes Mardi et il fait sec ce qu'on notera (S).
Si un jour, il fait sec, alors il fera sec le lendemain avec une probabilité de 5/6.
Si un jour, il fait humide ce qu'on notera (H), alors il fera humide le lendemain avec une probabilité de 2/3.
On s'intéresse au temps qu'il fera Jeudi.
Voici l'arbre de probabilité :
résumé du chapitre en vidéo:
exercice corrigé
résumé du chapitre sous format pdf