3ème chapitre 6:

I) Définitions

1) Hypoténuse, côté adjacent et côté opposé.

Dans le triangle ABC rectangle en B ci-dessous, on choisit un des deux angles aigus ( pas l'angle droit).

On prend par exemple l'angle BAC, et on définit le côté adjacent par rapport à l'angle choisi.

• le côté [AC] est le côté le plus long, c'est l'hypoténuse du triangle ABC. Il est toujours opposé à l'angle droit.
• Le côté [AB] est appelé côté adjacent à l'angle BAC. C'est le côté qui part de l'angle droit, mais qui n'est pas l'hypoténuse.
• Le côté restant, qui n'est ni l'hypoténuse, ni le côté adjacent, est appelé côté opposé à l'angle BAC ( car il est en face de l'angle choisi).
  

2) Cosinus, sinus et tangente d'un angle aigu

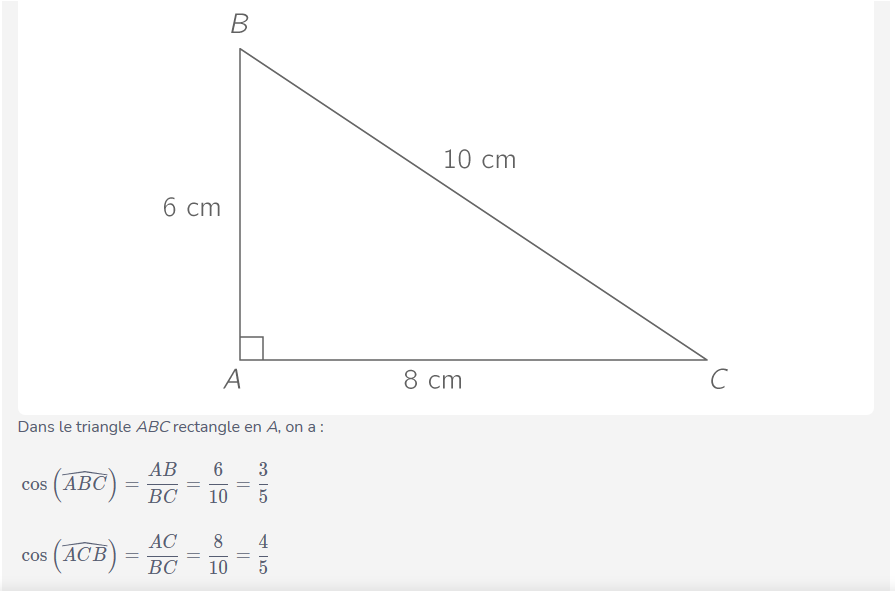
a) Dans un triangle rectangle,  le cosinus d'un angle aigu est égal à:

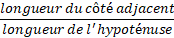
exemple 1 :

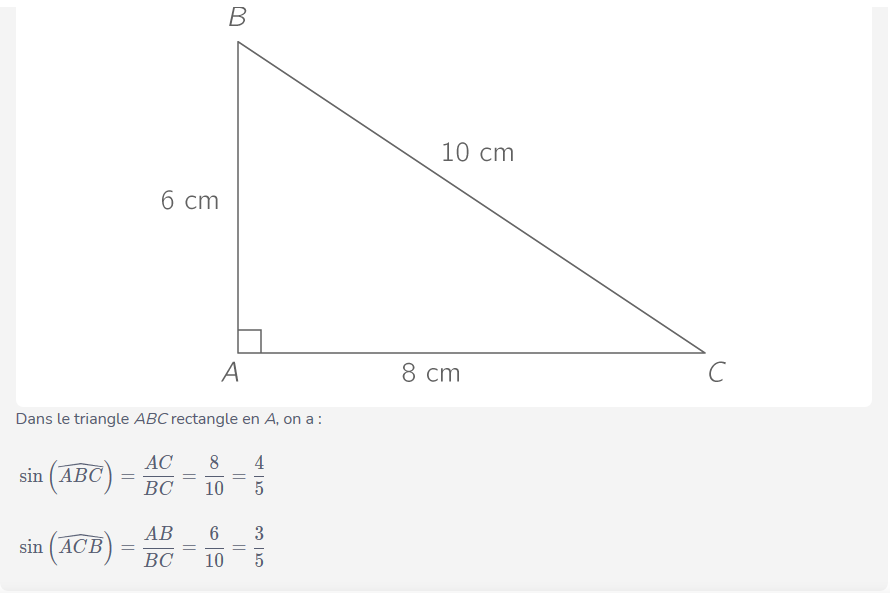
b) Dans un triangle rectangle, le sinus d'un angle aigu est égal à

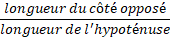
exemple 2:

Remarque:

On peut remarquer que :

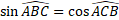
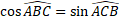
c) Dans un triangle rectangle, la tangente d'un angle aigu est égale à

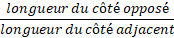
exemple:

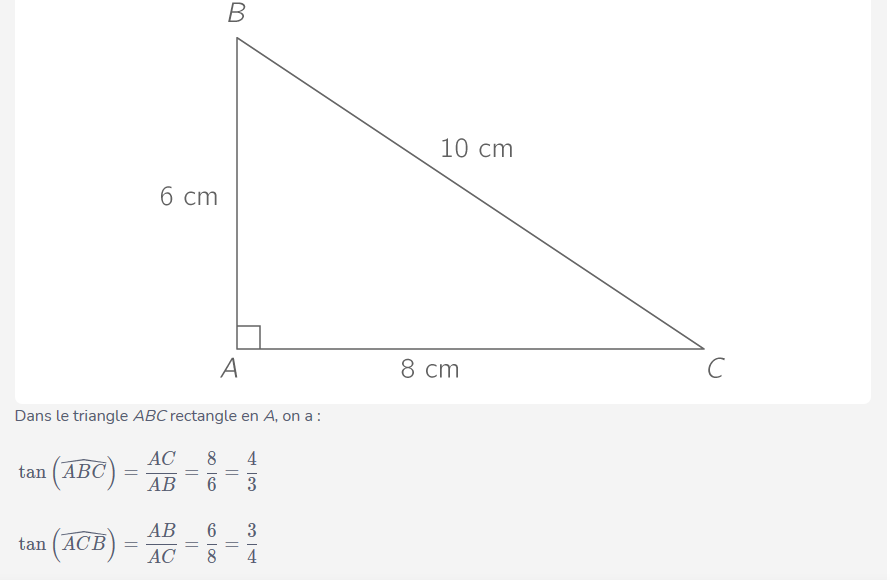
II) Propriétés

• le cosinus d'un angle aigu est toujours compris entre 0 et 1.
• le cosinus d'un angle aigu est toujours compris entre 0 et 1.
• la tangente d'un angle aigu est toujours supérieure à 0, mais pas nécessairement inférieure à 1.
  

La tangente peut aussi se calculer à partir du sinus et du cosinus:

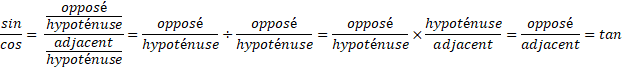
• il y a une relation entre le cosinus et le sinus ( liée au théorème de Pythagore):
  

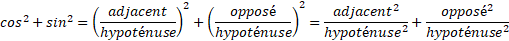
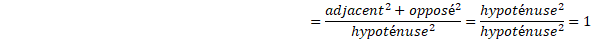
On peut alors calculer le sinus d'un angle connaissant le cosinus, et inversement.

exemple:

III) Applications

Nous allons maintenant utiliser les formules de trigonométrie que nous venons d'introduire dans des exercices classiques de calcul de longueurs et de mesures d'angles au sein de triangles rectangles.

1) Calcul de longueurs.

exemple 1:

Calculons  la mesure du segment rouge sachant que BC = 2,6 cm (arrondi au millimètre)

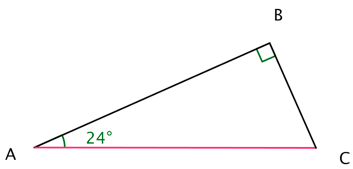
Dans le triangle ABC rectangle en B :

On cherche l'hypoténuse, et on connaît la longueur du côté opposé à l'angle A; on va donc utiliser le sinus.

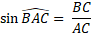
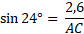
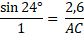
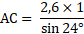
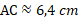
exemple 2:

Dans le triangle EFD rectangle en F, calculons la mesure du segment rouge [EF]  (arrondi au millimètre) sachant que DF = 3,7  cm 

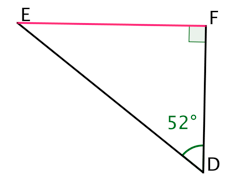
Dans le triangle EDF rectangle en F :

On a l'angle D, on cherche la longueur du côté opposé, et on connaît la longueur du côté adjacent à l'angle D; on va donc utiliser la tangente.

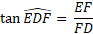
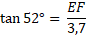
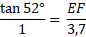
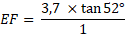
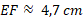
2) Calcul d'angles

a) La calculatrice

b) exemple :

Dans le triangle CDN, ci dessous, rectangle en N, calculer la mesure de l'angle D, arrondie au degré.

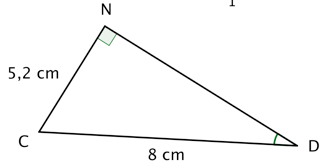
Dans le triangle NCD rectangle en N :

On cherche l'angle D, on a la longueur du côté opposé [NC], et on connaît la longueur de l'hypoténuse [DC]. On va donc utiliser le sinus.

En utilisant la calculatrice et la fonction arcsin(  ), on obtient :

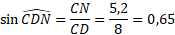
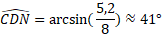
3) Résumé du cours et Exercices corrigés

fiche de cours synthétique à télécharger: